chaos_c

Auf den nächsten Seiten wird die weiter unten noch erfolgende schriftliche Ausarbeitung einer Unterrichtsreihe über Logistische Wachstumsdynamik und Chaos in der Jahrgangsstufe 10 in knappster Form beschrieben; diese Unterrichtsreihe hat der Autor in Unterrichtsprojekten und teilweise im Pflichtunterricht mit gutem Erfolg erprobt. Die vorgelegten Materialien verstehen sich insbesondere als ein Beitrag zum fächerübergreifenden Unterricht. Die Kurzbeschreibung der einzelnen Abschnitte soll interessierten LehrerInnen - auch solchen, die mit der Thematik noch nicht so vertraut sind - möglichst detailliert Auskunft über die zu behandelden Unterrichtsinhalte geben; daraus erklärt sich die relativ umfangreiche Beschreibung.

Ein kurzer Abstract im Teil D.- informiert weiterhin englischsprachige Interessenten.

Die vollständige schriftliche Ausarbeitung der Materialien umfaßt
74 DIN A-4 Seiten (WINWORD, MS-Office 98) und kann aus
Teil E.- heruntergeladen werden.

Die vorliegenden Materialien wollen einige grundlegende Aspekte in der Betrachtung dynamischer Systeme vermitteln, die zur Zeit mit Macht in den Unterricht der allgemeinbildenden Schulen drängen und die gleichermaßen für viele Wissenschaftsgebiete aber auch für Ansätze im fächerübergreifenden Unterricht eine erhebliche Bedeutung gewonnen haben.

Dynamische Systeme wie strömende Flüssigkeiten und Turbulenzen, Konvektionsströme und Zirkulationssysteme der Atmosphäre, Klimamodelle, oszillierende chemische Reaktionen, biologische Ökosysteme oder neurologische Systeme(z.B. Rhythmik der Herztätigkeit) reagieren mitunter - trotz deterministischer Modellbildung - auf kleinste Störungen völlig regellos und unberechenbar, weil diese Störungen durch nichtlineare Rückkopplungsmechanismen zu beherrschenden Faktoren des dynamischen Systems werden können(Lvz (9): (11)). Aufgrund vieler Einzelergebnisse und neuartiger Einsichten in den verschiedensten Wissenschaftsbereichen und nicht zuletzt mittels der enormen Möglichkeiten moderner Hochleistungsrechner konnte diese neue Betrachtungsweise seit etwa 1980 sicher Fuß fassen.

"Die Chaostheorie hat die Naturwissenschaften mit der überraschenden Tatsache konfrontiert, daß viele Phänomene trotz der Möglichkeit einer strengen und umfassenden deterministischen Modellierung prinzipiell nicht langfristig prognostizierbar sind. Entgegen unserer am mechanistischen Weltbild geschulten Intuition sind Systeme mit dieser Eigenschaft in der Natur darüber hinaus sogar offenbar die Regel und nicht die Ausnahme"
(Lvz (7), S. 1).

Im folgenden beschäftigen wir uns genauer mit Hilfe möglichst einfacher und anschaulicher mathematischer Hilfsmittel mit einigen wesentlichen Sachverhalten nichtlinearer Dynamik, aufgezeigt am Beispiel der logistischen Wachstumsgleichung. Das Unterrichtsmaterial ist für ca. 18 bis 19 Unterrichtsstunden im normalen mathematischen Pflichtunterricht der J-Stufe 10 bzw. 11.1 (mit deutlichem Schwerpunkt in der J-Stufe 10) konzipiert und setzt bei den SchülerInnen keinerlei Vorkenntnisse in nichtlinearer Dynamik voraus. Kürzungen von ca. 5/6 Unterrichtsstunden sind problemlos möglich. Ein zwangloser Einstieg in das Thema bietet sich an vielen Stellen des jeweiligen Jahrgangsstufenstoffes an, so u.a. bei Behandlung der Exponentialfunktion in der J-Stufe 10 oder später bei der möglichen Erarbeitung von Zahlenfolgen in der J-Stufe 11.1 (Lvz (3), (4)). Die mangelnden Vorkenntnisse der SchülerInnen und die knapp bemessene Unterrichtszeit haben zur Folge, daß die gewählten Beispiele, die Problemeinstiege und die benutzten Fachbegriffe viel einfacher und intuitiver ausgewählt und benutzt werden als dies in den meisten mir bekannten - oft auch für die Sekundarstufe II konzipierten - Unterrichtseinheiten über das vorliegende Thema üblich ist; mathematisch exakt gefaßte Begriffe fehlen deshalb ebenso wie ausgefeilte Lehrsätze und Beweise. Die mathematische Vorgehensweise hat mehr experimentellen und entdeckenden Charakter. Der besondere Reiz des vorliegenden Themas liegt u.a. in den vielen fächerübergreifenden Aspekten.

Die didaktisch-methodische Struktur der Unterrichtseinheit kann grob so beschrieben werden:

Nach der einfachen Analyse verschiedener Wachstumsmodelle werden mit Hilfe von Taschenrechnern und Computern vielfältige numerische Experimente zum logistischen Wachstum durchgeführt. Die zum Teil erstaunlichen numerischen Ergebnisse werden anschließend mit Hilfe des Verfahrens der Graphischen Iteration auf anschaulich-intuitive Weise analysiert und interpretiert. Anschauliche Betrachtungen zur Fehlerexpansion und Fehlerkompression sowie Betrachtungen zu fächerübergreifenden, unterrichtsimmanenten Anwendungsfeldern runden die Unterrichtsreihe ab. Zum Schluß wird ein Vorschlag zur Aufteilung der Einheit für 18/19 bzw. 13/14 Unterrichtsstunden gemacht.

Die Unterrichtseinheit basiert u.a. auf vielfältigen positiven Erfahrungen des Autors mit dem Thema Chaos(Deterministisches Chaos) im normalen Mathematikunterricht und in Projektwochen mit den verschiedensten J-Stufen am Luisen-Gymnasium in Düsseldorf, einer sog. Unesco-Projektschule (Themenschwerpunkt u.a.: Umwelt und globale Verantwortung); (Lvz (7), (8), (9), (10), (11)). Leitlinie bei all diesen Unterrichtsveranstaltungen (selbst in einem Leistungskurs) war immer, daß intuitives und entdeckendes Begreifen und Lernen absoluten Vorrang vor allen mathematisch begrifflichen Spitzfindigkeiten und Deduktionen haben muß.

Die vorliegenden Ausarbeitungen stützen sich zum Teil auf Peitgen, Jürgens, Saupe (5), (6), Reinartz (8), Lergenmüller (3), (4) des Lvz und eine Unterrichtskonzeption für die J-Stufe 10, die der Autor im Verlauf des Jahres 1995/96 im Rahmen seiner Mitarbeit für das Projekt MEDOS (Modellbildung/Exploration/Dynamik/Chaos und Simulation) des Landesinstituts für Schule und Weiterbildung des Landes Nordrhein-Westfalen in Soest erarbeitet hat. Eine genauere Beschreibung dieser Unterrichtskonzeption findet der interessierte Leser in Reinartz (11) des Lvz. Auf der Basis dieser Unterrichtskonzeption wurde vom Autor im Juni 1996 im Rahmen der Projektwoche ‘96 des Leibniz-Gymnasiums in Düsseldorf ein Projekt über grundlegende Aspekte der Chaostheorie erfolgreich durchgeführt.

Der enge Zeitrahmen im mathematischen Pflichtunterricht erlaubt zwar den Einsatz von Computern und programmierbaren Taschenrechnern, i.a.aber nicht die selbständige Erstellung von ablauffähigen Computerprogrammen durch die SchülerInnen zur Untersuchung der vielfältigen Aspekte des Themas Chaos. Die vorliegende Unterrichtskonzeption schließt aber Aktivitäten in diese Richtung selbstverständlich nicht aus. Aus den genannten Gründen werden deshalb für das Experimentieren am Computer ganz bewußt nur fertige Modellbildungssysteme und Computersoftware eingesetzt(Sw (1), (2), (3)).

Aus mathematischer Sicht ist die Iteration die Leitlinie für das vorliegende Unterrichtskonzept. Iteration paßt zum Computer, denn niemand kann besser iterieren als er. Der Begriff der Iteration wird bei der graphischen als auch bei der numerischen Iteration rein intuitiv erklärt und verwendet. Dabei soll die numerische und Graphische Iteration zunächst durch systematisches Probieren "per Hand" ausgeführt und ausgewertet werden("entdeckendes Lernen"). Die numerische Simulation am Computer soll dabei "Merkwürdigkeiten" zu Tage fördern, die erst durch die anschließende Analyse der Graphischen Iteration zufriedenstellend interpretiert und erklärt werden können. Dabei soll von den drei wesentlichen Charakteristika des Chaos, nämlich Mischen, Periodizität und Sensitivität, vor allem die Sensitivität den SchülerInnen ansatzweise vermittelt werden. Wichtig im Unterricht bezüglich der Sensitivität ist die Analyse und klare Abgrenzung zwischen linearer und nichtlinearer Dynamik.

Ein weiteres wesentliches Ziel der vorgestellten Unterrichtseinheit ist, daß mit einfachsten mathematischen Hilfsmitteln wesentliche Sachverhalte nichtlinearer Dynamik und ihre Konsequenzen für ein angemessenes Verhalten im Umgang mit der Natur und Umwelt einsichtig gemacht werden. Wenn auch z.B. ein sehr vereinfachtes mathematisches Klimamodell in den Jahrgangsstufen 10 oder 11 noch nicht besprochen werden kann, so leidet darunter aber keineswegs die Einsicht in den gesamten Problemkreis, weil die zu behandelnde logistische Wachstumsgleichung bekanntlich die wesentlichen Strukturen von Chaos generiert. Der angemessene Transfer der Strukturen und Ergebnisse des logistischen Wachstumsprozesses auf andere nichtlineare Dynamiken und die Diskussion über die sich daraus ergebenden Konsequenzen für unser eigenes Verhalten (Beispiel Klimaproblematik und Klimamodelle) sollte gerade auch im Hinblick auf die Forderung nach fächerübergreifendem Unterricht den SchülerInnen unbedingt zugemutet werden. Bezüglich der oben erwähnten Sensitivität sollte insbesondere deutlich werden, daß viele der real existierenden Öko -und Klimasysteme etc. äußerst empfindlich auf menschliche Eingriffe reagieren können, unter Umständen mit katastrophalen Folgen. Diese Aspekte können zum Schluß der Unterrichtsreihe vertieft oder in deren Verlauf unterrichtsimmanent behandelt werden.

Die Auseinandersetzung mit der Nichtlinearität in unserer Welt bedeutet eine Erziehung zum dringend notwendigen vernetzten, nichtlinearen Denken und insbesondere eine Erziehung zur globalen Verantwortung(Lvz (9), (10), (11), (12)). Schon deshalb verstehen sich die Materialien auch als ein praktischer Beitrag zum anwendungsorientierten und fächerübergreifenden bzw. projektorientierten Unterricht.

Neben einem kurzen historischen Abriß werden die wesentlichen Erkenntnisse und Folgerungen aus der Chaostheorie in allgemeiner Form dargestellt. Kurz diskutiert werden auch die für uns notwendigen Konsequenzen im Umgang mit Natur und Umwelt, die sich aus der Chaostheorie ergeben.

Ausgehend von einem einfachen Zinsbeispiel wird das diskrete lineare Wachstum als Wachstum mit konstantem Zuwachs auf eine lineare Iterationsformel zurückgeführt.:

Schon hier - aber auch später bei der logistischen Gleichung - wird eine begriffliche Klärung und Trennung von linearer und nichtlinearer Dynamik vorgenommen. Das gleiche Zinsbeispiel dient nun als Ausgangspunkt für die Einführung des Zinseszinses und damit des exponentiellen Wachstums, eines Wachstums mit bestandsproportionalem Zuwachs. Auch das diskrete exponentielle Wachstum wird auf eine lineare Iterationsformel zurückgeführt:

Das "explodierende" Wachstum macht langfristig eine Beschränkung erforderlich. Aber wie sollte diese Beschränkung aussehen? Diskutiert werden einige Möglichkeiten, so z.B. das Modell von Lottka-Volterra(Lvz (3)). Eine sinnvolle Möglichkeit, exponentielles Wachstum zu besckränken, ist nun u.a. das Modell des logistischen Wachstums von P.F. Verhulst (1845), bei dem die Wachstumsrate von der momentanen Populationsgröße abhängig ist. Die Herleitung des logistischen Wachstums aus dem Modell des exponentiellen Wachstums führt im zeitdiskreten Fall auf eine nichtlineare Iterationsformel; diese Nichtlinearität wird sich noch als bedeutsam herausstellen. Aus Gründen der Vergleichbarkeit verschiedener Populationen und der mathematischen Vereinfachung wird die sog. Standardform der logistischen Gleichung benutzt:

Erste Vermutungen über den graphischen Verlauf einer logistischen Zeitreihe führen auf eine sog. S-Kurve(Sättigungskurve).

Nach Anfertigung eines einfachen Programms für die logistische Wachstumsgleichung lassen sich mit beliebigen programmierbaren Taschenrechnern schon recht interessante und aufschlußreiche numerische Experimente durchführen. Untersucht wird die Gleichung

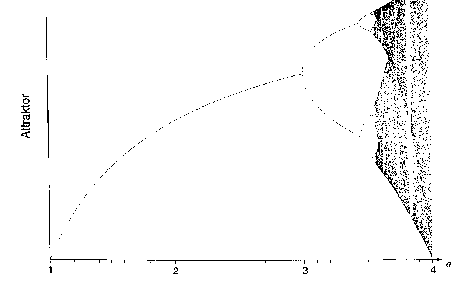
Der Taschenrechner offenbart bei genauerer numerischer Untersuchung das bekannte Feigenbaum-Szenario; Graphik-Taschenrechner produzieren entsprechend ein Feigenbaumdiagramm (ein Feigenbaumdiagramm in Gegenüberstellung von entsprechender Zeitreihe und graphischer Iteration erfolgt im fortlaufenden Text weiter unten).

Für 3,56999 Ð r Ð 4 (chaotischer Bereich) wird mit zwei nur geringfügig sich unterscheidenden Startwerten x₀gestartet ("Schmetterlingseffekt").

Zwei Taschenrechner verschiedener Fabrikation rechnen für
3,56999Ð rÐ 4 mit exakt gleichen Startwerten x₀ und führen langfristig auf völlig verschiedene Iterationswerte. Was ist der wahre Orbit?

Ein Taschenrechner rechnet für 3,56999 Ð r Ð 4 mit ein und demselben Startwert x₀ die Iterationswerte einmal mit x_n+1 = r x_n (1 - x_n ) und dann mit x_n+1 = r x_n - r x_n ² aus; langfristig führt auch dies zu völlig verschiedenen Iterationswerten. Was ist hier der wahre Orbit?

Die erstaunlichen Ergebnisse in allen drei Experimenten sind direkte Folgen der Sensitivität im chaotischen Parameterbereich für r. Wegen der begrenzten Stellenzahl "macht Chaos jeden Computer nieder".

Für 3,8284 £ r £ 3,8425 werden periodische Fenster ("Inseln der Ordnung") gesucht.

Im Anschluß an diese Taschenrechnerexperimente werden Computer eingesetzt, um mit Hilfe des Modellbildungssystems MBS-LLC(Lvz (12), Sw (1)) Zeitreihen für die logistische Wachstumsgleichung in einem Koordinatensystem zu erzeugen und die Graphik zu analysieren. MBS-LLC ist ein gleichungsorientiertes Modellbildungssystem mit dessen Hilfe einfache, aber auch komplexere Modelle Dynamischer Systeme auf dem Computer implementiert werden können; das Modell für logistisches Wachstum liegt schon fertig implementiert vor. MBS-LLC ist bei fertig implementierten Modellen auch von SchülerInnen ohne Eingewöhnungszeit sehr einfach zu bedienen und auf MS-DOS-Rechnern lauffähig. Selbstverständlich lassen sich an dieser Stelle alternativ auch graphikorientierte Systeme wie z.B. MODUS(unter MS-DOS) oder DYNAMSYS(unter WINDOWS) einsetzen. Möglich wäre aber auch der Einsatz einer Tabellenkalkulation oder eines Computeralgebrasystems wie z.B. DERIVE (vgl. Lergenmüller Lvz (4)).

Mit Hilfe von MBS-LLC wird der gesamte Bereich für 0 Ð r Ð 4 numerisch systematisch untersucht und die gewonnenen Zeitreihen analysiert und interpretiert. Dabei ergeben sich intuitiv fast zwangsläufig die Begriffe Fixpunktattraktor, periodischer Grenzzyklusattraktor, chaotischer(seltsamer) Attraktor, Feigenbaumbifurkation und periodisches Fenster. Die erhaltenen Ergebnisse erlauben die Bestimmung der Feigenbaumkonstanten d . Weiterhin werden mit Hilfe des WINDOWS-Programms FIGWIN(Sw (2)) Feigenbaumdiagramme erstellt und analysiert. Die Anwendung einer Zoomfunktion ermöglicht die ziemlich genaue numerische Bestimmung der Feigenbaumkonstanten und belegt die fraktale Struktur der "Feigenbäume". Entsprechend kann auch das Programm FRACTINT verwendet werden(Sw (3)).

Es erhebt sich die Frage, was der tiefere Grund für das zum Teil erstaunliche Verhalten der Zeitreihen, das sich natürlich auch in der Struktur des Feigenbaumdiagramms widerspiegelt, ist. Die Beantwortung dieser Frage wird in den folgenden Abschnitten mit Hilfe des Verfahrens der Graphischen Iteration angegangen.

Nach Einführung des Graphischen Iterationsverfahrens für die logistische Wachstumsparabel wird mit Hilfe von Arbeitsblättern(Lvz (6)) die Graphische Iteration für verschiedene logistische Parabelversionen mit variierenden Startwerten und unterschiedlichen Fragestellungen von den SchülerInnen per Hand vorgenommen und die Ergebnisse anschließend analysiert und mit den Ergebnissen der Zeitreihenanalyse mittels MBS-LLC 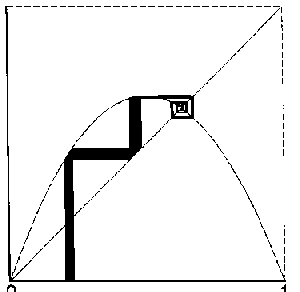verglichen. Dabei ergibt sich, daß bei Veränderung von kleinem r (flache Parabel) zu großem r (steile Parabel) die Art der Iterationsspiralen sich entsprechend den jeweiligen Ergebnissen der Zeitreihenanalyse verändert und zwar vom Fixpunktattraktor über den Grenzzyklusattraktor zum chaotischen Attraktor. Der Begriff des abstoßenden Fixpunktes (Repeller) ergibt sich jetzt sofort anschaulich aus der Art des Iterationspfades. Auch das graphische Iterationsverfahren offenbart mit Hilfe von Arbeitsblättern für r=4 die Sensitivität im chaotischen Bereich. Selbst bei immer gleich gewählten Anfangswerten x₀ und gleichbleibender Wiederholung des Verfahrens erhalten die meisten SchülerInnen jetzt in der Regel völlig verschiedene Iterationspfade. Da sich aber solche Iterationspfade nicht beliebig weit voneinander entfernen können, kommen sie sich nach einer gewissen Anzahl von Iterationsschritten auch wieder beliebig nahe, so daß die Iterationspfade schließlich das Definitionsintervall der Parabel und damit auch die Fläche unterhalb der Parabel dicht mit einem Spinngewebe ausfüllen(Mischen).

Es wird allergrößter Wert darauf gelegt, daß die Graphische Iteration per Hand mit Hilfe von Arbeitsblättern durchgeführt wird, um den SchülerInnen ein tieferes Verständnis über das Iterationsverfahren zu ermöglichen. Es wird also bewußt darauf verzichtet, zur Anwendung des graphischen Iterationsverfahrens fertige Computerprogramme einzusetzen, obwohl diese in ausreichender Qualität existieren.

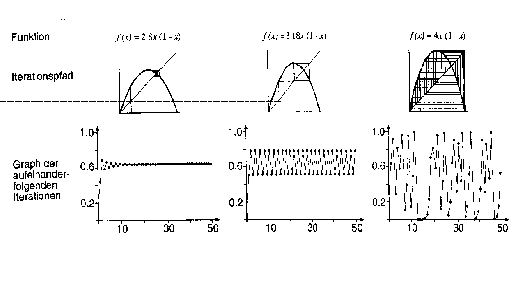
Eine Gegenüberstellung von Zeitreihen, Feigenbaumdiagrammen und Iterationspfaden für jeweils festes r vertieft abschließend die Erkenntnis über die Zusammenhänge:

Offensichtlich ist jetzt, daß das logistische Wachstumsverhalten von der Steilheit der Parabel, die sich über den Parameter r steuern läßt, abhängig ist. Nötig ist nun ein genaueres Kriterium in Verbindung mit der Steilheit der Parabel und einer Überlegung, warum die Nichtlinearität der logistischen Wachstumsgleichung eine so große Rolle spielt. Dies leistet die Analyse der Graphischen Iteration bei linearen Systemen (lineare Dynamik).

Mit Hilfe von Arbeitsblättern wird die graphische Iteration per Hand u.a. für die Geraden f(x) = 2 x; f(x) = - 0.5 x; f(x) = - 2 x; f(x) = 0.5 x durchgeführt. Die SchülerInnen kommen leicht selbst zu folgenden Erkenntnissen:

"Bei linearen Systemen ist die Dynamik des Systems vom Steigungsverhalten der Geraden und damit vom Steigungsfaktor m abhängig. Die Steigung m der verwendeten Geraden bestimmt den Charakter des Iterationspfades und man kann dabei vier Fälle unterscheiden, nämlich":

"In linearen dynamischen Systemen ist das Auftreten von Chaos nicht möglich, aber: Nicht in jedem nichtlinearen System steckt Chaos".

Überträgt man die Erkenntnisse aus der linearen Dynamik lokal auf die logistische Parabel(genauer auf die Tangente, die durch den theoretischen Fixpunkt verläuft), so erhält man für die Parabel lokal bezüglich der anziehenden und abstoßenden Fixpunkte ähnliche Kriterien wie für eine Gerade:

Die Benutzung des Tangenten -und Ableitungsbegriffs ist natürlich in der Jahrgangsstufe 10 und eventuell auch in der Stufe 11.1 noch nicht möglich. Entweder verwendet man stattdessen eine intuitiv-anschauliche Erklärung oder man führt eine geometrische Betrachtungsweise ein, wie sie Hofstadter in (2), S. 383 des Lvz vorschlägt.

zum Inhaltsverzeichnis von Teil C.

Ein wichtiger Aspekt ist der Effekt, den die Iteration auf kleinste Fehlerintervalle hat; diese kleinsten Fehlerintervalle dienen als Modell für Eingabefehler. Diesen Effekt kann man schon vorher mit Hilfe der Arbeitsblätter für die Graphische Iteration bei linearen Systemen und bei der logistischen Parabel leicht erkunden. Diesen Effekt erfaßt man aber intuitiv auch sofort bei der bloßen Betrachtung und Untersuchung von Graphiken zur Fehlerexpansion -und Kompression:

Numerisch kleine Fehler blähen sich auf, wenn Intervalle unter Iteration expandieren (Fehlerexpansion); sie werden noch kleiner und ziehen sich auf Null zusammen, wenn sich die Intervalle zusammenziehen (Fehlerkompression).

Fehlerexpansion findet statt, wenn die Parabel steil ist( ç m ç > 1); Fehlerkompression findet statt, wenn die Parabel flach ist( 0 £ ç m ç < 1 ).

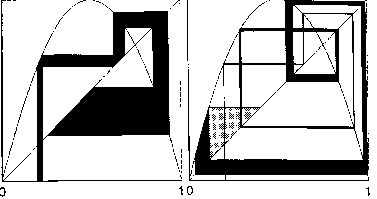
Veranschaulichung der Sensitivität durch Graphische Iteration: Intervallkompression(oben) und Intervallexpansion(unten)

Sensitivität im chaotischen Bereich bedeutet für die logistische Parabel, daß dicht zusammenliegende Anfangswerte total verschiedene Iterationsfolgen erzeugen. Dadurch blähen sich auch kleinste Fehlerintervalle gewaltig auf; diese können aber nicht beliebig wachsen und werden deshalb wieder auf sich "zurückgefaltet". Fehlerexpansion und Fehlerkompression wechseln einander ab; eine Folge davon ist das ziellose Verhalten des Orbits auf dem ganzen Definitionsintervall, wobei im Falle der Graphischen Iteration die Iterationspfade ein Spinngewebe bilden (Mischen).

zum Inhaltsverzeichnis

zum zweiten Teil von C. Kurzbeschreibung der Inhalte und Materialien
einer Unterrichtsreihe für die Jahrgangsstufe 10